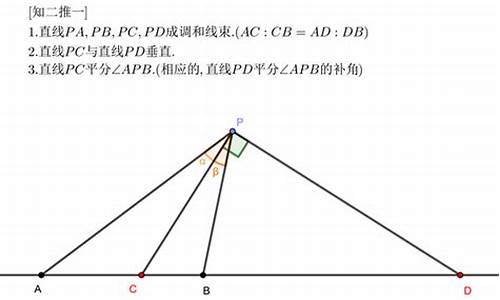
您现在的位置是: 首页 > 教育科技 教育科技
江苏高考数学第20题,2020江苏高考数学23题
tamoadmin 2024-06-16 人已围观
简介1.2011江苏高考数学20题第二问详解你怎么做的啊这个变态难,前两问我做了15分钟,还剩15分钟,没攻得下第三问。现在网上有答案了。(2)可以做的,直接用a1(a2)和d。a1*a3^3=a2^4,a2^2*a4^4=a3^6,第二个式子开根号a2*a4^2=a3^3,代入第一个式子a2^3=a1*a4^2=(a2-d)(a2+2d)^2,解之,a2^2=4/3d^2,a2两个值,一个不满足a4
1.2011江苏高考数学20题第二问详解你怎么做的啊

这个变态难,前两问我做了15分钟,还剩15分钟,没攻得下第三问。现在网上有答案了。
(2)可以做的,直接用a1(a2)和d。
a1*a3^3=a2^4,a2^2*a4^4=a3^6,
第二个式子开根号a2*a4^2=a3^3,代入第一个式子
a2^3=a1*a4^2=(a2-d)(a2+2d)^2,解之,a2^2=4/3d^2,a2两个值,一个不满足a4>0,另一带入一式不成立(其实都不成立)
(答案方法更好)
(3)答案的思路:以d为自变量,证明只有d=0成立,从而矛盾。
先齐次化,在齐次式将a1和d同除以a1,变为单变量式。
之后消去参数n,k。途径是在指数式中取自然对数。然后变为单变量方程,设函数,改为研究函数零点。
思路难想,后来那个求导也难算。但是如果功底深厚,这些不过是一些常规的操作,华山自古一条道,就当是一个积累。
楼主考得如何
2011江苏高考数学20题第二问详解你怎么做的啊
第1到10题:填空题。
第11题:函数与导数,根据题目意思求函数的极值小值点即为零点,求到a的值即可求函数最大值与最小值.
第12题:根据题目意思设点,利用垂直得到等量关系.即可解决
第14题:方法众多,考查基本不等式.
第14题:等差与等比数列前N项和公式的应用,可用列举法解决.
第15题:立体几何证明平行与垂直,难度不大.
第16题:三角函数的和差公式、二倍角公式的应用.不难,但基础功底要厚实.
第17题:三角函数的实际应用,函数与导数求最值
第18题:圆锥曲线问题:其实是常规题,计算上有一定要求,在平常考试中也就这样的题目了.并不偏.
第19、20题:不盼着都拿满分,好歹这题是有区分度的,满分很难,但得到一定的分数还是比较简单的。
高考数学压轴题难度规律:
1、高考中的压轴题通常第一问和第二小问是第三问的解题关键,所以第一问和第二问也是第三问的基础。第一问与第二问的计算通常会有简便,但是又不会轻易想到的办法。
2、高考中数学的压轴题型基本上是固定的几种,所以这时候有针对的练习是有作用的,而这几种题型的一个基本特点就是灵活,设置灵活,解题灵活,思路灵活。
3、最后一道题目的计算量通常较大,考升往往会在一边想思路,但是又一边计算着繁琐的题目中失去耐心。
既然有人给你解答了,我就讲一下思路。
第1问就不写了。
第2问道理差不多,首先要相信只有等差数列才能同时满足那两个条件,在这个前提下大胆猜测结论,然后就是证明。高考难度通常比较低,中学生知识又少,要相信结论只能是很简单的。
先把条件用一遍
n>3时(S_{n+3}-S_{n})+(S_{n}-S_{n-3})=2S_3,即
a_{n+3}+a_{n+2}+a_{n+1}-a_{n}-a_{n-1}-a_{n-2}=2S_3 (*)
把n用n+1代之后和这个式子减一下得到
a_{n+4}-2a_{n+1}+a_{n-2}=0,即a_{n+4}-a_{n+1}=a_{n+1}-a_{n-2}
这样就得到了第一类的三组间隔为3的等差子列A_1={a_2,a_5,...}, A_2={a_3,a_6,...}, A_3={a_4,a_7,...}
同理把k=4的条件
a_{n+4}+a_{n+3}+a_{n+2}+a_{n+1}-a_{n}-a_{n-1}-a_{n-2}-a_{n-3}=2S_4 (**)
用一遍可以得到第二类的四组间隔为4的等差子列B_1={a_2,a_6,...}, B_2={a_3,a_7,...}, B_3={a_4,a_8,...}, B_4={a_5,a_9,...}
并且注意除a_1外{a_n}的任何一项必同时属于某个A_u和某个B_v。
下一步证明每一类内部的几个等差数列的公差是一样的,因为3和4互质,做到这里应该已经可以相信结论一定是对的。
用(**)-(*)得到a_{n+4}-a_{n-3}=2a_4,也就是说又得到一类间隔为7的等差子列。假定A_u的公差为d_u,那么对于任何a_n属于A_u,利用7d_u=a_{n+21}-a_{n}=6a_4,所以d_u=6/7*a_4,即第一类的三组序列的公差相同,简记为d。同理考察a_{n+28}-a_{n}得第二类的四组序列公差也相同,简记为D,其大小为D=2a_4。
(如果没有想到(**)-(*)这步,那么可以考察a_{n+12}-a_{n},注意a_{n}可以取遍所有的A_u和B_v,可以得到d_u和D_v和u,v无关,只不过无法直接得到d,D及a_4的关系)
下一步目标就很明确了,证明整个{a_n}(第一项除外)就是等差数列,同样是从两类序列的公共点着手,取几个特殊点解方程即可。
利用
a_8 = a_2+2d = a_4+D
a_10 = a_2+2D = a_4+2d
解出d/3=D/4,再代入 a_{n+4} = a_{n}+D = a_{n+1}+d 即得从a_2开始{a_n}是等差数列且公差为D-d。
最后结合前面的d=6/7*a_4, D=2a_4即得D=8,d=6,a_4=7,从而得到a_n=2n-1,这恰好对第1项也成立。
(如果前面没想到(**)-(*)那步的话就把(*)变形成3d=2S_3,把(**)变成4D=2S_4,也可以解出同样的结论。总之最后一步纯粹是解线性方程组,已经不用动脑子了,大不了多取几个点)